What is Linear Discriminant Analysis and Quadratic Discriminant Analysis?

Linear Discriminant Analysis or LDA is a statistical technique for binary and multiclass
classification. It too assumes a Gaussian distribution for the numerical input variables.

 

A quadratic classifier is used in machine learning and statistical classification to separate measurements of two or more classes of objects or events by a quadric surface. It is a more general version of the linear classifier.

Both are used dimension reduction to smaller but discriminative components.

Discriminant analysis is a composite procedure with two distinct stages – dimensionality reduction (supervised) and classification stage. At dimensionality reduction we extract discriminant functions which replace the original explanatory variables. Then we classify (typically by Bayes’ approach) observations to the classes using those functions.

Differences between LDA and QDA?

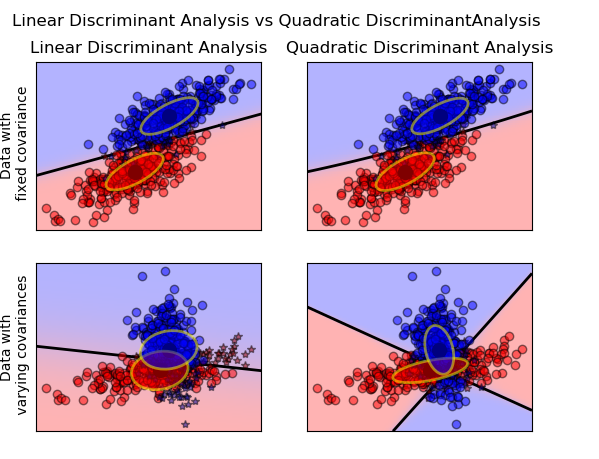
1. Linear Discriminant Analysis can only learn linear boundaries, while Quadratic Discriminant Analysis can learn quadratic boundaries and is therefore more flexible. Link

2. QDA can perform better in the presence of a limited number of training observations because it does make some assumptions about the form of the decision boundary.

3. QDA assumes a quadratic decision boundary, it can accurately model a wider range of problems than can the linear methods.

4. LDA is a much less flexible classifier than QDA.

References –

http://scikit-learn.org/stable/modules/lda_qda.html

http://people.math.umass.edu/~anna/stat697F/Chapter4_2.pdf

https://stats.stackexchange.com/questions/169436/how-lda-a-classification-technique-also-serves-as-dimensionality-reduction-tec

Linear and Quadratic Discriminant Analysis for ML / statistics newbies
Read more

Transfer Learning with various architectures of Convolutional Networks.

http://ruder.io/transfer-learning/

ImageNet: VGGNet, ResNet, Inception, and Xception with Keras

 

Transfer learning & The art of using Pre-trained Models in Deep Learning

http://torch.ch/blog/2016/02/04/resnets.html

ResNet, AlexNet, VGG

http://cv-tricks.com/cnn/understand-resnet-alexnet-vgg-inception/

http://kaiminghe.com/icml16tutorial/icml2016_tutorial_deep_residual_networks_kaiminghe.pdf

https://github.com/KaimingHe/deep-residual-networks

http://www.learngroup.org/uploads/2015-04-01/Solution_Manual_Artificial_Intelligence_A_Modern_Approach.pdf

 

Code – https://towardsdatascience.com/transfer-learning-using-keras-d804b2e04ef8

https://harishnarayanan.org/writing/artistic-style-transfer/

https://www.pyimagesearch.com/static/ppao-sample-chapter.pdf

 

https://github.com/phpmind/TensorFlow-Tutorials-1

Read more

Bootstrapping:
To understand bootstrap, suppose it were possible to draw repeated samples (of the same size) from the population of interest, a large number of times. Then, one would get a fairly good idea about the sampling distribution of a particular statistic from the collection of its values arising from these repeated samples. The idea behind bootstrap is to use the data of a sample study at hand as a “surrogate population”, for the purpose of approximating the sampling distribution of a statistic; i.e. to resample (with replacement) from the sample data at hand and create a large number of “phantom samples” known as bootstrap samples.
In other words, We randomly sample with replacement from the n known observations. We then call this a bootstrap sample. Since we allow for replacement, this bootstrap sample most likely not identical to our initial sample. Some data points may be duplicated, and others data points from the initial may be omitted in a bootstrap sample.
An Example:
The following numerical example will help to demonstrate how the process works. If we begin with the sample 2, 4, 5, 6, 6, then all of the following are possible bootstrap samples:
2 ,5, 5, 6, 6
4, 5, 6, 6, 6
2, 2, 4, 5, 5
2, 2, 2, 4, 6
2, 2, 2, 2, 2
4,6, 6, 6, 6

Bagging:
Bootstrap aggregating (bagging) is a machine learning ensemble meta-algorithm designed to improve the stability and accuracy of machine learning algorithms used in statistical classification and regression. It also reduces variance and helps to avoid overfitting. Although it is usually applied to decision tree methods, it can be used with any type of method

Read more

Some of the useful Ubuntu commands along with its descriptions. This might be used as a handy reference to quickly know about the syntax of a command.

Command Description
wget URL Downloads the file specified by the URL.
pwd Displays the current directory you are in.
sudo Allows the user to act like a superuser
sudo -i Allows the user to get root access.
sudo apt-get install package_name Allows the user to act like a superuser and install packages
cd directory_name Changes from current directory to the mentioned directory.
cd .. Moves back one directory
ls To view the contents in a directory including files and sub-directories.
ls -a To view the contents in a directory including hidden files.
man command Displays the information about the command specified.
whereis file/directory Shows where the specified file/directory is.
mkdir directory_name Creates a directory with the given name.
mv oldname newname Renames the file.
rm filename Removes the specified filename.
rmdir directoryname Removes the specified empty directory.
rm -r directoryname Removes files and sub-directories in the specified directory.
ifconfig & iwconfig Allows the user to look at the network configuration.
ping URL Allows the user to test connectivity issues.
vi filename Opens the specified file in the vi editor to view/make changes.
telnet ip_address Connects to the specified IP address.
chmod 777 file_name Modifies the permissions of the specified file.

  • 4 – Read
  • 2 – Write
  • 1 – Execute
  • 0 – No permissions

The three digits in 777 represents users, groups and others.
7 means – 4 + 2 + 1, meaning users can read, write and execute.
chmod -R 777 directory Modifies the permissions of the specified directory recursively. Meaning it applies the changes for all the files and sub-directories.
Read more

Fermi questions are questions designed to test your logic, and you may have encountered them before. So, they usually are formed or phrased in a way where the person asking you this question designs a scenario, asks you about a real world scenario, and asks you to provide an estimate very quickly. Here are few examples. Try to solve these 🙂

 

 

http://www.physics.uwo.ca/science_olympics/events/puzzles/fermi_questions.htm

http://mathforum.org/workshops/sum96/interdisc/sheila1.html

http://mathforum.org/workshops/sum96/interdisc/fermicollect.html

http://mathforum.org/workshops/sum96/interdisc/classicfermi.html

 

 

Read more

What is an eGPU?
GPU stands for Graphics Processing Unit, which is more commonly referred to as a Video Card or Graphics Chip. The “e” prefix stands for “external”. In short, an eGPU is the act of hooking up a desktop video card to a laptop, or a SFF system lacking actual desktop-sized slots (such as an Intel NUC).

But why?! Wouldn’t a desktop make more sense? Wouldn’t a desktop erform better?
Why not? Maybe. Most of the time.

To elaborate:
Not all people want a desktop. Desktops are (typically) large, (typically) bulky and (by definition) immobile. There is convenience in having your own system with you on the road, while still being able to game in the comfort of your own home, without having to sync any data, or switch systems. One system is convenient, two are less so.

That said, if there is no particular wish to use a single machine, or if a laptop is not needed/desired in the first place, a desktop machine is undeniably superior (and often cheaper, if we compare the price of a laptop+eGPU setup to the price of a desktop built from scratch). There are a few considerations that make eGPUs desirable: Already owning a laptop (often a high-end one, for example, due to the requirements of an occupation) and wishing to be able to game on it, having an older laptop that could use a little boost in the arm in the graphics department but is otherwise perfectly usable, and saving space (because an eGPU plus a laptop take up very little space and are easier to fit into a small apartment or a dorm).

A desktop system with a near top-of-the-line desktop CPU (like the Intel i7 6700K or i5 6600K) and a given video card will nearly always outperform a laptop (no matter how high end the laptop is) with the same video card connected as an eGPU. This is an undeniable fact. However, eGPU performance can range from ~70% to ~95% of the equivalent desktop performance (depending on how the eGPU is connected to the laptop, whether you are using the internal or an external display, the game in question, the resolution you are at, as well as the frame rate you are getting), so the performance is still definitely there and is definitely viable………………………………………….   More

Source – https://www.reddit.com/r/eGPU/comments/5jpf2x/diy_egpu_101_introduction_to_egpu/

Read more